作者 |特里斯坦·李约瑟 [美国] (Tristan Needham)

来源 | “可视化微分几何和形式：五幕数学剧”

译者：刘伟安

这一结果导致了数学和物理学的一些根本性进展，其中一些我们已经触及，而另一些则必须等到后面的章节。 1868年，贝尔特拉米用这个结果解释了双曲几何是具有恒定负高斯曲率的鞍形表面的内在几何。这一解释是关键的一步，为双曲几何被普遍接受铺平了道路。黎曼将高斯的固有曲率扩展到高维流形。 1915年，爱因斯坦利用黎曼的杰作，提供了准确表达广义相对论的数学形式。这个表达极其精确和优美，其中引力被理解为物质和能量对时空的压力，形成时空固有几何中的曲率。

然而，为了正确理解这个奇妙的定理本身，我们首先讨论它的起源。 Dombrowski（1979）在这方面做了精彩而深刻的工作。通过查阅高斯的私人笔记本、给朋友的信以及官方出版物，他仔细地拼凑了一份年表，反映了高斯对微分几何一般见解的发展，特别是对这个定理的见解的发展的影响。正如 Dombrowski 所解释的那样，高斯的史诗般的探索始于 1816 年，当时他对曲面曲率做出了非局部的发现，这一发现既深刻又出人意料。

高斯美丽的定理（1816）

高斯是一个不喜欢炫耀的人。虽然他很少称赞别人，但至少他不是一个伪君子。直到他去世之前，他的一系列重大发现都被隐藏在他的私人笔记本中，因为他认为结果还不够完美，无法公开发表。事实上，他的拉丁语座右铭是 pauca, sed matura，意思是“虽小，但成熟”。 1816 年的这一非本地结果就是这些未发表的发现之一。

麻烦的是，即使在他的私人笔记本①中，高斯也没有留下任何线索告诉人们他是如何猜出这个结果以及如何证明的，但他却异常兴奋地想出了这个名字：

这里高斯所说的“球面图像”是指曲面通过球面映射到S 2 上的图像。图13-1用香蕉皮来说明这个定理的含义。我们强烈鼓励您亲自尝试这个（或类似的）实验。

首先，我们从香蕉的正曲率一侧切一条缝，将香蕉从皮中取出，并保持香蕉皮完整。在负曲率的一侧画一个逆时针的盒子，在这个盒子上垂直于香蕉皮插入一根牙签，代表垂直的法向量。

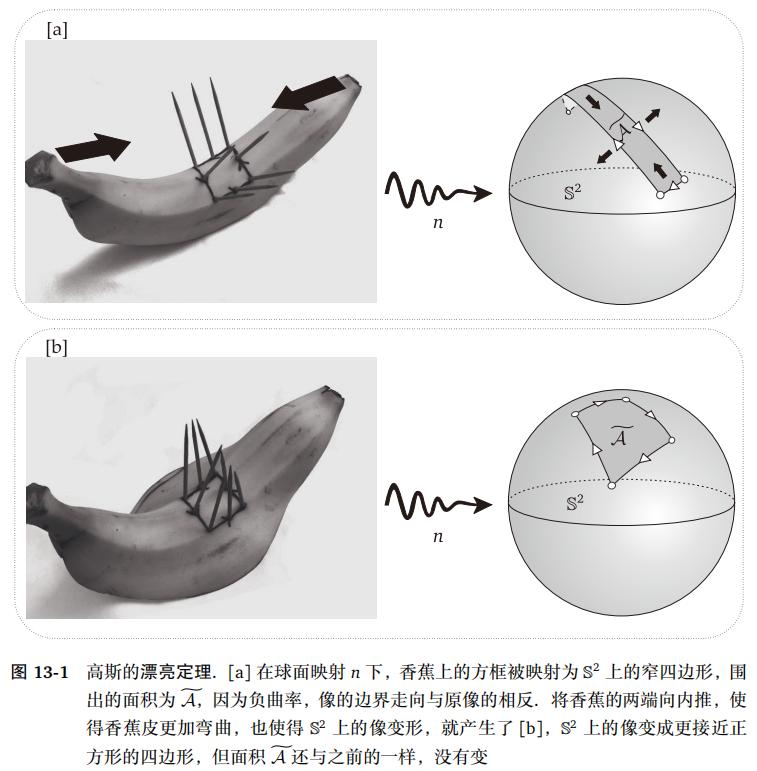
在球形映射下，该框被映射到由

一个狭窄的四边形，其边界

方向与原图像相反，如图13-1a所示。一定要用眼睛顺着香蕉皮上方框的方向，确认法向量的尖端确实与上图中的方向相反。

现在将香蕉的两端向内推，香蕉皮会发生等轴变，我们之前画的盒子也会变形，得到的图像更接近正方形。根据美丽定理，这个新的球面图像的面积与变形前相同。

这样的实验让我们真正看到定理（13.1）的潜在数学真理，这确实令人兴奋，但它们并没有解释太多。在第四幕中，我们将介绍平行运动的概念。借助平行运动，可以为这个美丽的定理提供概念性的解释。现在我们只能先承认这一点，才能推导出后续的结果——精彩的定理。

高斯辉煌定理 (1827)

在发现这个美丽定理后的10年里，高斯确实从未发表过任何关于它的信息。然而，私下里，他多次回到微分几何和他美丽的定理，特别是在1822年和1825年，写出完整的手稿，然后突然放弃。

终于，1827年，他终于心满意足，出版了以此成果为核心内容的《曲面通论》，压抑已久的兴奋得到了释放。

此前，他曾私下称其为“美丽的定理”。现在，他以“奇妙的定理”的形式向全世界宣布了这一点。然而，到了这个时候，高斯几乎完全掩盖了他在1816年发现非局域结果的痕迹，以纯粹局域的形式将结果呈现给世人。只需简单地将美丽定理中的图简化为p点，你就可以理解他是如何获得这个结果的新的局部解释的。

设曲面S上点p包围的面积为δA，其在曲面上的像是包围点n(p)的球面，面积为

．从逻辑上讲，δA在S的等距变换下是不变的。根据美丽定理（13.1），它也是不变的。因此，我们立即得到以下精彩定理：

实验。将香蕉两端向内推，看看p点处香蕉皮会发生什么变化：曲率半径ρ1收缩（因为这个主方向与香蕉的方向相同），十字的曲率半径ρ2 -截面标记变大。根据定理（13.2），在香蕉皮的弯曲过程中，乘积ρ1ρ2始终保持相同的常数。

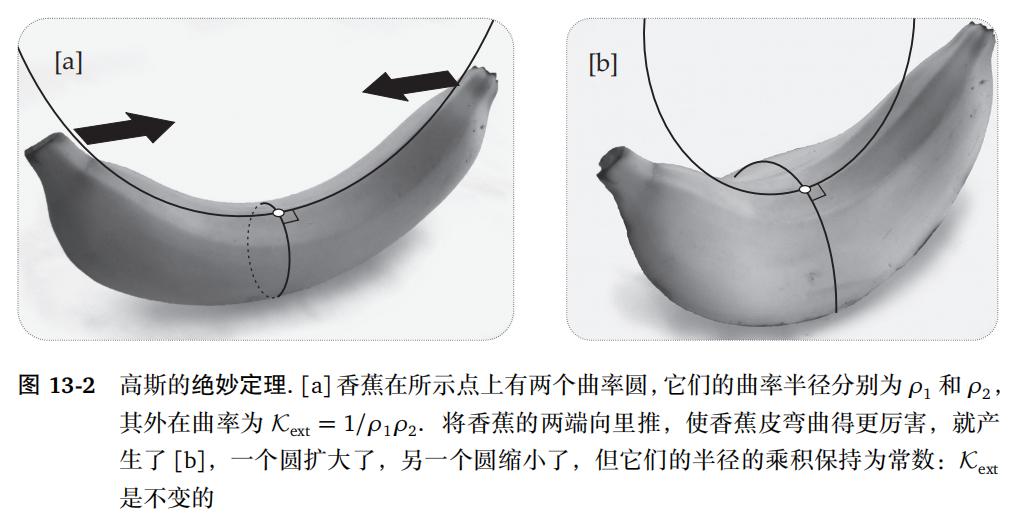
为了验证这个结论，取两根相对较硬（容易成型）的金属丝，在香蕉上选择一个特定的点，然后弯曲金属丝，直到它在特定点的两个主要方向上自然地粘在香蕉上（不要还没有做）。将香蕉从香蕉皮）表面取出，得到此时两个主曲率圆的圆弧。然后将这两个圆弧平放在桌子上，测量它们的半径ρ1和ρ2，并得到乘积ρ1ρ2。然后，请朋友弯曲香蕉并保持稳定。和之前一样，在同一点上，让金属丝自然地粘附在香蕉新曲面上的两个新主方向①上。最后，在实验误差范围内，验证新产品ρ1ρ2与之前相同。

这里的“弯曲”意味着连续变形，但这并不是定理的实际要求：确实存在一些等距变换无法通过温和且连续的等距变形来实现。根据定理，这样的等距变换仍然保持曲率不变。

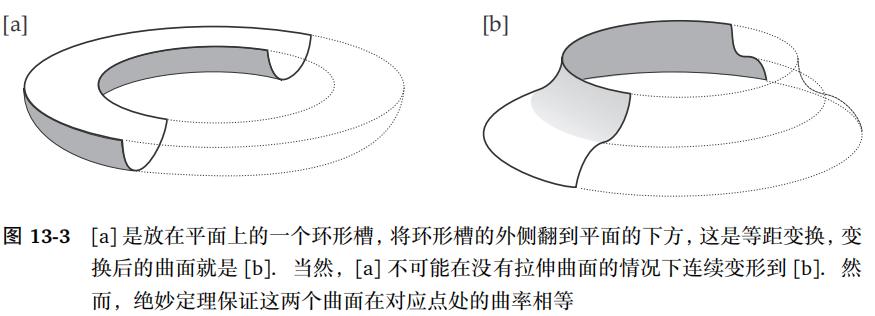
我们用 Aleksandrov 著作中的一个例子来说明这一点（Aleksandrov，1969，第 101 页）。图13-3是Alexandrov的手绘原图。图13-3a描绘了一个环形凹槽。想象它放在一个平面上，与平面的接触就是圆周C。将环形槽沿圆周C切成两部分，然后将外半圆翻转过来，与内半圆粘在一起，得到图13-3b。显然，新曲面与原始曲面等距，但直观上显而易见（并且可以证明）的是，如果原始曲面是刚性的，则它无法在不拉伸的情况下弯曲成新曲面。注意，如果是直槽（半圆柱面），在不拉伸的情况下连续变形即可得到新的曲面。

当谈论弯曲时，术语“表面”在物理和数学中是不同的。物理表面，无论多薄，在不拉伸的情况下几乎不可能弯曲。例如，取一张矩形纸，将其卷起，然后将卷起的两个边粘在一起以获得圆柱面。纸张原来的边长相等，但圆筒的外周比内周稍长，因此外侧必须被拉伸，在材料中产生张力。正是由于这个原因，当我们撕掉胶带时，纸张就会弹回原来的平整状态。只是在数学上，曲面没有厚度，可以弯曲而不拉伸。

高斯的结果（13.2）已经很优秀了，但还有进一步的发展。这个奇妙的定理表明，Kext 实际上是曲率的内在度量。自然，我们要问：它与第19页方程（2.1）中高斯曲率K的原始内在定义有什么关系？当时用单位面积的余角来定义，即KE(Δ)/A(Δ)。

高斯的回答甚至更好：

根据这个结果，我们可以忽略两种曲率定义的差异，直接将其称为曲面的曲率K。这是在下面完成的。

至于美丽定理，这个奇妙结果的最简单、最普遍的证明要等到第四幕介绍平行运动时才会介绍。然而，在下一章中，我们将能够通过涉及多面体的有限论证使这个结果更加可信。

接下来，我们将针对一些特殊曲面验证结论（13.3）的有效性。对于这些曲面，我们已经通过计算知道了它们的外在主曲率和内在高斯曲率。

• 圆柱形和圆锥形表面。本质上平坦的平面可以卷成圆柱体或圆锥体，因此这两种类型的表面的高斯曲率为零。结合这个事实和结论（12.5），我们有

• 球体。结合第 8 页的结论（12.4）和方程（1.3），我们有

• 伪球体。结合第 60 页的结论（10.9）和结论（5.3），我们有

• 环面。结合结论（10.10）和第 104 页的练习 23，我们有

这五种曲面在历史和数学中都非常重要，因此我们将一一描述它们，但实际上，所有五种曲面都服从结论（13.3）这一事实可以一起表述如下。

• 一般旋转表面。结合结论 (10.11)(10.12) 和第 103 页的练习 22，其中粒子以单位速率沿母线移动，我们有

可视化微分几何和形式：五幕数学剧

作者：【美】特里斯坦·李约瑟

译者：刘伟安

点击封面图片购买本书↑↑↑

1. 旧金山大学数学系教授、理学院副院长、博士牛津大学博士论文，诺贝尔奖得主罗杰·彭罗斯、霍金的弟子特里斯坦·李约瑟的经典代表作！

2、200多张手绘示意图，让“微分几何”回归“几何”，用牛顿几何方法对经典结果给出几何解释。

3.原版豆瓣评分高达9.9！被认为是“像小说一样流畅的数学教科书！”

4、译者为国内著名偏微分方程专家，武汉大学原校长齐民友、武汉大学数学教授刘伟安的弟子。

“复杂分析：可视化方法”