审稿人：努尔

这是一个典型的教科书问题：当你的汽车没油时，你需要多大的力来推动它加速到给定的速度？牛顿第二运动定律的答案是：F=ma，其中a是加速度，m是质量，F是力的大小。这个非常直接和优雅的定律描述了各种各样的运动。至少理论上它可以回答世界上所有的物理问题。

真的吗？当人们开始从很小的尺度思考世界时，比如电子围绕原子核旋转，他们意识到一切都变得非常奇怪，牛顿定律似乎不再适用。要描述这个微观世界，需要使用二十世纪初发展起来的量子力学。该理论的核心是薛定谔方程，可以类比经典力学中的牛顿第二定律。

波与粒子

“在经典力学中，我们用位置和动量来描述物理系统的状态，”剑桥大学理论物理学家纳齐姆·布瓦塔 (Nazim Bwata) 解释道。例如：你有一张桌子，上面有许多可移动的台球。只要知道某个时刻t每个球的位置和动量（动量是质量乘以速度），就可以知道此时的系统。 t的所有信息：所有物体的运动状态和速度。 “我们会问：如果我们知道系统的初始状态，即知道系统在t时刻的状态，那么系统的状态会如何演化？我们可以用牛顿第二定律来解决这个问题。在量子力学中，如果你问同样的问题，答案很棘手，因为位置和动量不再是描述系统的合适变量。”

问题的关键是：量子力学试图描述的物体及其行为并不像一个小台球那么简单。有时最好将其想象为波浪。 “以光为例，除了引力方面的研究之外，牛顿对光也很感兴趣。”博伊塔说，“根据牛顿的理论，光可以被描述为一种粒子。但后来，根据许多其他科学家的说法，它通过研究，包括詹姆斯·克拉克·麦克斯韦提供的理论理解，我们发现光是用波来描述的”。

但在 1905 年，爱因斯坦意识到波动图也不太正确。为了解释光电效应，您需要将光束想象为粒子流，爱因斯坦将其称为光子。光子的数量与光强成正比，每个光子的能量与频率成正比：

在

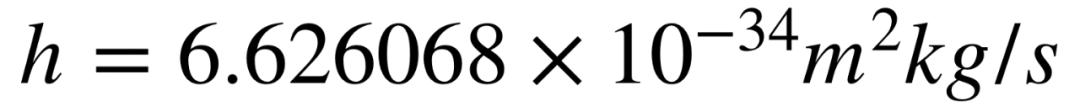
，它是普朗克常数，一个非常小的常数，以马克斯·普朗克的名字命名，他在 1900 年关于黑体辐射的工作中猜出了这个公式。“我们现在面临的问题是，描述光的正确方法有时是波，有时是波作为一个粒子，”博伊塔说。

爱因斯坦的成果可以与科学界长期的努力联系起来，从 17 世纪的克里斯蒂安·惠更斯开始，一直到 19 世纪的威廉·汉密尔顿。他们都想统一光的波动性质。和粒子物理学。受到光在不同情况下的特性的启发，年轻的法国物理学家路易斯-维克多·德布罗意在这次探索之旅中迈出了激动人心的一步：他假设不仅光，物质也具有这种可能性，被称为波的特性——粒子二象性。物质的基本组成部分（例如电子）在某些情况下也表现得像粒子，在某些情况下也表现得像波。

路易斯·德布罗意，1892-1987。

德布罗意1920年提出的观点与其说是基于实验证据的猜想，不如说是受爱因斯坦相对论启发的理论飞跃。但没过多久，科学家们就发现了相应的实验证据。 1820 年代末，粒子被晶格散射的实验证实了电子的“波状”性质。

证明波粒二象性最著名的实验是双缝干涉实验。在这个实验中，电子（或其他粒子，如光子或中子）被喷射并同时穿过带有两个狭缝的屏幕。该屏幕后面还有另一个屏幕，用于检测电子通过狭缝后最终到达的位置。但您在检测屏幕上实际看到的是干涉图案：只有假设电子是波，您才会看到这种图案。波同时穿过两个狭缝，然后在沿一个方向传播时与自身发生干涉。然而，在检测屏幕上，当电子第一次到达时，它会被视为粒子，这正是我们所期望的。事实上，这个看似奇怪的结果是一个已经被重复了无数次的实验事实——所以我们必须接受这就是世界运转的方式。

双缝干涉实验：波穿过狭缝的干涉图样

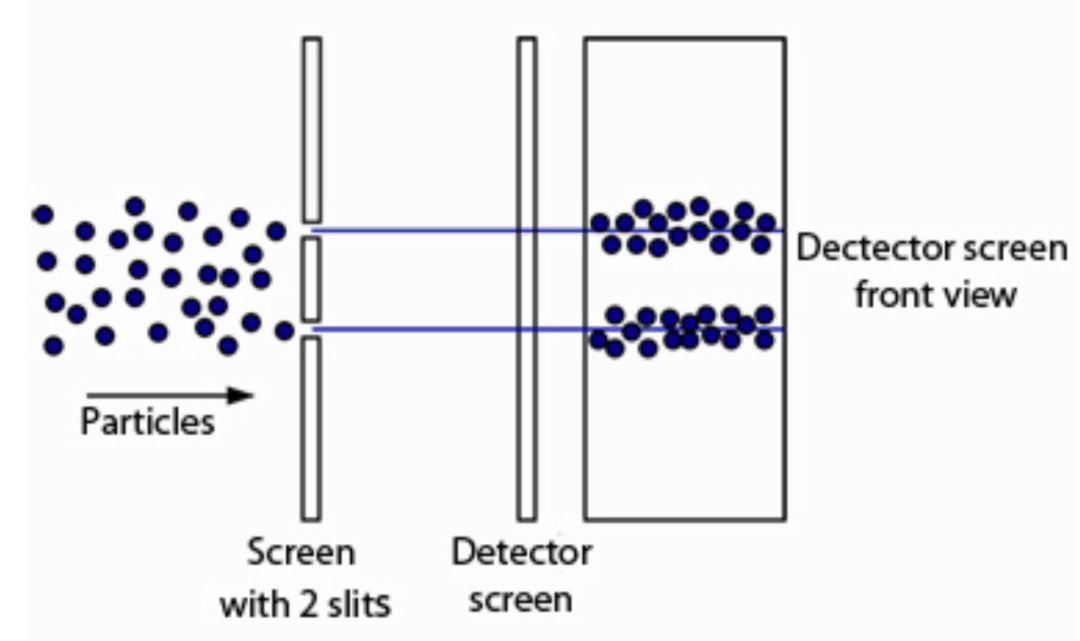
双缝干涉实验：当粒子通过缝发射时会发生什么

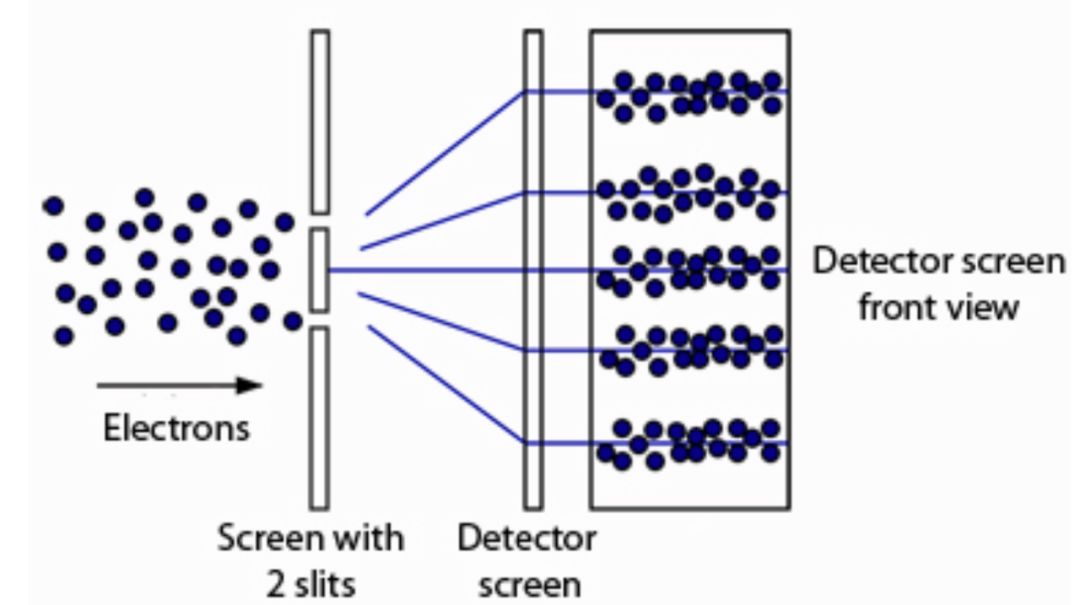
双缝干涉实验：当粒子（例如电子）穿过狭缝时实际发生的情况：你会得到波状干涉图案，但电子以粒子形式到达。

薛定谔方程

德布罗意提出的新图像需要新的物理学。与粒子相关的波的数学形式是什么？爱因斯坦通过以下公式将光子的能量 E 与光波的频率 f 联系起来

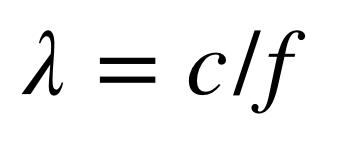
我们知道频率与波长有关。这里c是光速。利用相对论的结果，我们可以将光子的能量与其动量联系起来。根据以上结论，可以给出波长λ与光子动量p的关系：

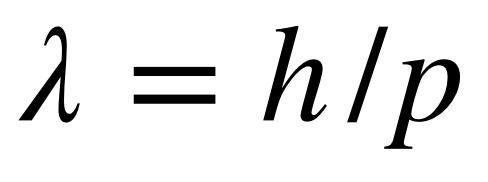
其中 h 是普朗克常数。

基于此，德布罗意假设波长和动量之间的关系对于任何粒子都成立。此时，最好放弃你的直觉，不要去思考粒子表现得像波意味着什么，而只是遵循数学逻辑。

在经典力学中，波（例如声波和水波）随时间的演变是通过波动方程来描述的：一个微分方程，其解是一个波函数，它给出了在任何时间受到适当边界条件影响的波的形状。

例如，假设波沿着 x 方向延伸的弦传播，并在 xy 平面中振动。为了完整地描述这种波，您需要知道 t 弦在每个 x 点和每个时刻在 y 方向上的位移。利用牛顿第二运动定律，可以看出波动方程如下：

v 是波速。

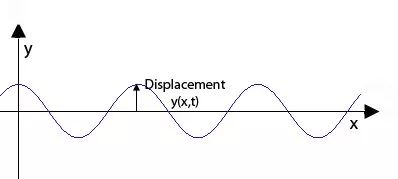
上图是一根弦在xy平面上振动的照片。这里的波可以用余弦函数来描述。

上述方程的通解相当复杂，反映了弦可以以多种方式摆动的事实。并且您需要更多信息（初始条件和边界条件）来弄清楚它是什么类型的运动。但是，举个例子，

该函数描述了以角频率 ω 沿正 x 方向传播的波，那么正如您所期望的，它是波动方程的可能解。

薛定谔方程以薛定谔 (1887-1961) 的名字命名。

同样，应该有一个波动方程来控制神秘物质波随时间的演化。它的解决方案应该是一个波函数（不要将其视为实际的波），它一次告诉您有关量子系统的所有信息（例如：在盒子中移动的单个粒子）。奥地利物理学家埃尔温·薛定谔于1926年提出了这个方程。对于在三维空间中运动的单个粒子，方程可以写成如下：

其中 是粒子的势能，是 x、y、z、t 的函数，m 是粒子质量，h 是普朗克常数。方程的解是波函数 ψ (x, y, z, t)。

在某些情况下，势能不依赖于时间 t。在这种情况下，我们通常通过考虑更简单的与时间无关的薛定谔方程来解决问题，其中ψ(x,y,z)仅取决于空间，使得以下关系成立：

E 其中 是粒子的总能量。那么整个方程的解为：

这些方程可以应用于在三维空间中移动的单个粒子。也有相应的方程来描述具有任意粒子的系统。除了将波函数写为位置和时间的函数之外，我们还可以将波函数写为动量和时间的函数。

进入不确定性

我们可以从一个简单的例子开始求解薛定谔方程，比如单个粒子在无限深的势阱中运动，它的解与描述波的数学方程非常相似。

这个解决方案意味着什么？它既不给出粒子在给定时刻的精确位置，也不给出粒子随时间变化的轨迹。更准确地说，它给出给定时间所有可能位置 (x, y, z) 的值 ψ (x, y, z, t)。这个值是什么意思？ 1926年，物理学家马克斯·玻恩提出了一种统计解释。他假设波函数的绝对值的平方

将给出在时间 t 的位置找到粒子的概率密度。换句话说，粒子在时间 t 出现在某个区域的概率由以下积分给出：

这张概率图与德布罗意关于粒子波长和动量的公式有着惊人的联系。海森堡于 1927 年发现，测量运动粒子的位置和动量时，精度存在根本性限制。一个人在某一方面想测量得越精确，在其他方面就越难说。这不是指测量仪器的质量，而是指自然界固有的不确定性。这个结果现在被称为海森堡的不确定性原理，并且是经常用来引用量子力学奇怪现象的几个结果之一。这意味着在量子力学中我们不能谈论粒子的位置或轨道。

维尔纳·海森堡，1901-1976。

布瓦塔说：“如果我们相信不确定性图景，因为我们对‘电子当时在哪里’等问题没有明确的答案，换句话说，量子态和状态的所有数学表示只能给我们概率结果” 。 “德布罗意、薛定谔和爱因斯坦试图对真空中传播的光波提供现实的解释。然而，泡利、海森堡和玻尔等一些物理学家反对给出现实的解释图像。对他们来说，波函数只是计算概率的工具。”

真的适用吗？

我们为什么要相信这个奇妙的想法？在这篇文章中，我们提出了薛定谔方程，就好像它是从空中摘下来的一样，但它实际上是从哪里来的呢？著名物理学家理查德·费曼认为这是一个毫无意义的问题：“我们从哪里得到这个方程？它不能从你知道的任何东西中推导出来。它来自薛定谔的大脑。”

然而，这个方程到目前为止已经经受住了所有的实验。 “这是量子力学中最基本的方程，”博伊塔说。 “这是我们想要描述的所有量子力学系统（例如电子、质子、中子等）的起点。”这个方程在前期是成功的。描述氢原子的离散能谱有助于量子力学的建立，这也是薛定谔的动机之一。根据欧内斯特·卢瑟福的原子模型，氢等原子发出的光的频率应该是连续的。然而，实验表明它不会连续变化。氢原子只发射特定频率的光，当频率变化时会出现跳跃。这一发现与传统的哲学智慧背道而驰，传统的哲学智慧支持了十七世纪哲学家和数学家戈特弗里德·莱布尼茨表达的格言：“自然不会跳跃。”不跳跃）”。

1913 年，尼尔斯·玻尔提出了一种新的原子模型，其中电子被限制在特定的能级。薛定谔将他的方程应用于氢原子，发现他的解完全重复了玻尔设定的能级。 “这是一个令人兴奋的结果，也是薛定谔方程的首批重大成就之一，”博伊塔说。

由于无数成功实验的支持，薛定谔方程已成为量子力学中牛顿第二定律的模拟和替代。