编译|七七

体育课来了数学老师，数学老师一来，校队就直接拿了世界级奖牌？像这样的幻想联系是真实的，并且可能成为体育界的常态。

事情要从美国泳圈的“体量”说起。

数学教授创造奇迹

在美国，游泳是一项非常流行且“量大”的运动。美国人口超过3.3亿，但每年约有300万儿童参加夏季游泳联赛活动。美国游泳圈有一句座右铭：“吃、睡、游”（eat、sleep、swim）。这听起来是不是很像东亚版“吃、睡、游”的美国镜像？这也反映了那个游泳世界的纪律和单调。

美国泳池卷曲到什么程度了？事实上，进入美国大学游泳队是一项值得夸耀的成就。因为根据美国大学体育协会（NCAA）的统计，只有7%的高中游泳运动员能够入选NCAA一级。

但要进入国家队，这个水平还远远不够。每届奥运会游泳比赛，全美只有60-80名运动员可以获得美国奥运国家队资格赛的邀请，其中只有4人能够进入国家队。

正是因为国内的成功，美国游泳队才成为世界强队。根据2023年Speedo世界排名，女子100米蛙泳前五名中，有4名美国运动员。

在世界级的比赛中，最强者之间的差距往往只有百分之一秒。毫不夸张地说，厘秒的差别就可以将一个玩家从“大师村”送到“退休村”。

为了与时间赛跑，一位美国大学队教练想到请数学老师“代课”。

这位教练是美国体校实力雄厚的弗吉尼亚大学女子游泳队的托德·德索博（Todd DeSorbo），他聘请的数学老师是研究数论的小野肯（Ken Ono）。小野是该校数学系的教授。他的“主要领域”是数论和解析函数，例如模形式。

数学对游泳有多大贡献？那我们还是要用数学来说话。

自从小野在2020-2021赛季成为弗吉尼亚大学游泳队顾问以来，该队不仅赢得了首枚全国金牌，而且卫冕成功，开启了全国四连冠之旅。近年来，每一位在世界级比赛中获得金牌的美国女运动员都来自弗吉尼亚大学小野队。

世界冠军来自弗吉尼亚大学的克莱尔·柯赞 (Claire Curzan) 和凯特·道格拉斯 (Kate Douglass) |数学智力家

在小野的指导下，运动员们也经常创造新的个人最好成绩。

例如，几年前加入弗吉尼亚大学游泳队的凯特·道格拉斯(Kate Douglass)最初以2分30秒的成绩创下了200米蛙泳的个人纪录，但现在她以2分30秒的时间成为了美国纪录保持者。 2分19.3秒。今年她成为巴黎奥运会夺冠热门。

女运动员克莱尔·柯赞从斯坦福大学转学到弗吉尼亚大学后，在短短几个月的训练中就在50米、100米和200米蛙泳中创造了新的个人最好成绩。

在今年的美国大学生锦标赛上，弗吉尼亚大学的格雷琴·沃尔什在100米蝶泳项目中打破了世界纪录，该校的佩奇·马登在400米自由泳项目中获得银牌。她也将第二次赢得奥运会冠军。

包括凯特·道格拉斯在内，今年弗吉尼亚大学的九名队员将代表美国队参赛。要知道，仅这所学校的运动员就占了美国游泳队的五分之一。

总体而言，弗吉尼亚大学游泳队的记录比美国任何其他大学都多。 2023年接受哥伦比亚广播公司采访时，小野自豪地表示，弗吉尼亚大学在游泳方面取得的成就堪称一个国家独树一帜。

夺金的关键

那么，运动员如何利用数学训练呢？

许多人不知道的是，游泳运动员的成功或失败很大程度上取决于他们“游”得有多好，而是取决于他们不游泳时的表现。如果在水下“滑翔”时保持正确的姿势，不仅可以减少阻力，还可以给自己发力的机会。

这是因为人体实际上并不是为游泳而设计的。例如，旗鱼可以轻松达到每小时130公里的速度，但奥运会运动员的速度只有旗鱼的十分之一。这主要是因为人类在水下移动时，克服阻力的能力不如鱼类。

小野表示，减少阻力是夺金的关键。为了做到这一点，运动员们不惜一切代价，例如剃掉体毛或穿着特殊的泳衣。 2024年美国游泳队的泳衣太紧，一些女运动员需要半个小时才能穿上。

由于水的阻力与物体的面积成正比，因此运动员必须“雕塑”身体肌肉以减少阻力。这就是所谓的倒V形游泳者体型的由来。为了让身体变得更加流线型，一些运动员还会进行瑜伽训练，让身体变得柔软，能够“弯”成阻力最小的姿势。

但阻力最小的位置到底是什么？这就是数学发挥作用的地方。

用数学来指导运动，听起来很高端，但其实原理并不复杂。小野表示，他使用的分析方法是基于牛顿力学，并将相关公式应用到运动员身上。他需要测量的主要内容是加速度、减速度和阻力。

事实上，小野一开始的硬件条件相当“草根”。

起初，他使用了专门为鲨鱼设计的加速度计，然后用保鲜膜将仪器绑在运动员的腰部。但有的运动员体力太强，器械总是被挤掉。为此，小野的妻子特意帮他制作了一条可以固定探测器的腰带。有些探测器对光敏感，因此必须用抗紫外线的塑料薄膜包裹。

当然，后来他的条件好了很多，最近又收到了手力传感器等高端设备。

运动员手上佩戴的力传感器丨数学智能

运动员腰间佩戴的测量仪丨数理智能

动态图像也很重要。小野捕捉运动员游泳的高清视频。此外，小野还记录了运动员的灵活性、疲劳程度、不同节奏踢球时的表现等。

利用这些数据，他们对每位运动员进行了分析，例如找到不需要减速的区域、头部的不正确位置、疲劳对划桨的影响、力量的损失以及身体是否朝着正确的方向奔跑。这些微小的细节或许只能带来百分之一秒的差别，但在奥运会的赛场上，却将决定胜负。

为玩家打造“数字双胞胎”

现在，小野只需要看看两名运动员的加速度数据，就可以轻松判断出谁更强，而无需观看实际比赛。

例如下图中，黄色玩家的动作更加流畅，因为她的加速度数据在0附近振荡，这是因为她遇到的阻力很小。相比之下，蓝色选手的滑行就逊色很多。

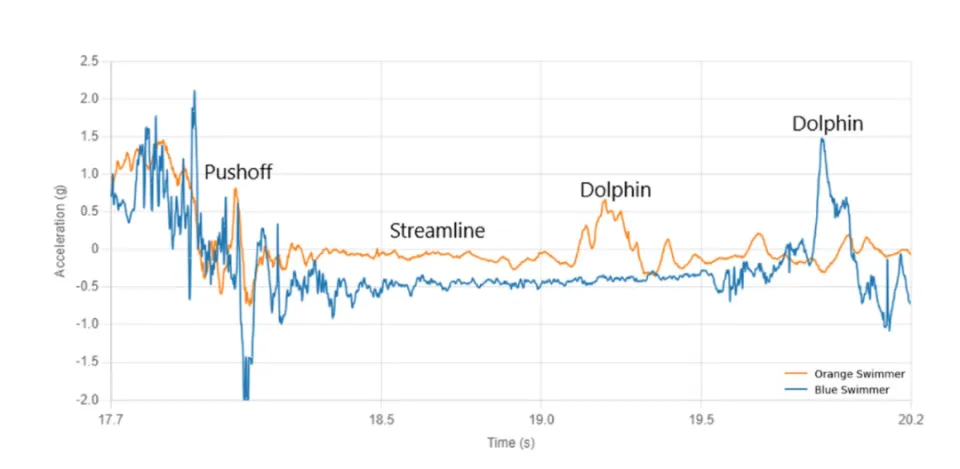
两位不同能力运动员的加速度对比丨数理智能

当然，让运动员一次又一次尝试、犯错误的成本太高了。小野想到了一个更好的办法，那就是利用数据打造运动员的“数字双胞胎”。这些数字虚拟人可以量化运动员的失误，为真人训练提供具体、精准的指导。

例如，在200米蛙泳项目中，运动员一般会滑行4次。如果你能在滑翔时调整态度以减少阻力，你将获得0.4-0.6秒的进步。

上面提到的凯特·道格拉斯(Kate Douglass)在开始滑翔时头部姿势错误，因此受到了很大的阻力。在虚拟人的帮助下，经过 36 个月的训练，道格拉斯每次滑行时间缩短了 0.11 秒，在 200 米蛙泳中总共快了 0.44 秒。这个进步看似不大，但却直接帮助她打破了保持了20年的美国纪录。

凯特·道格拉斯 (Kate Douglass) 一开始阻力很大的头部姿势之前丨数学智能

凯特·道格拉斯用数学调整头部姿势丨数学智能

借助数字孪生，研究人员还可以让他们的克隆人参与各种“训练”，并在运动员休息时实施不同的战术。

例如，是否增加“蝴蝶踢”的次数，可以通过数字孪生来回答。

蝴蝶踢

要知道，游泳比赛中一个非常消耗体力的动作就是“蝶泳”。这个动作做得好的话可以加速0.1秒，但是需要非常高的有氧能力。如果达不到实际效果，教练员和运动员是不会轻易增加的。这就是为什么传统教练不建议进行多次蝶泳，而世界顶级选手的蝶泳次数一般不超过20次。

但小野的数字孪生提出了不同的建议。例如，弗吉尼亚大学女队的克莱尔·柯赞(Claire Curzan)在2020年美国公开赛上完成了10+11蝶泳，获得了蝶泳冠军。

有了不怕苦、不怕疲劳的数字孪生，教练可以评估运动员是否有能力增加蝶泳，以及通过增加蝶泳可以提高多少成绩，从而制定新的训练方向。

过去七八年里，小野收集了100多名顶尖运动员的游泳数据。根据这些数据创建的数字双胞胎之间的战斗结果可以测试不同的策略，例如转动时手放在哪里以及呼吸多少次。

数字模拟器还可以模拟游戏的进程。例如，你的对手可能一开始就领先，但你可以预测，当他们减速时，你会在第三圈超越他们。

利用小野给出的游泳“公式”，弗吉尼亚大学游泳队在比赛中占据了主导地位。小野自豪地说，在美国大学生锦标赛上，弗吉尼亚大学游泳队拥有无敌的优势。早在2021年奥运会赛场上，就有四名美国运动员拥有数字双胞胎进行“训练”，并且每人都获得了一枚奖牌。

更令人惊奇的是，数字孪生还可以用作绘图工具。

事实上，凯特·道格拉斯在被数学天才看中之前从未考虑过蛙泳项目，因为她在中学时的蛙泳成绩并不是顶尖水平。

但凭借小野的分析技术，教练得知她的身体素质和有氧代谢都是世界一流的，道格拉斯超越了自己的极限，仅仅36个月后就刷新了美国蛙泳纪录。

对于未来，小野相信他的团队现在使用的数据技术和测量方法将成为常态：“五年后，我们的故事将只是一个故事，每个人都会做我们正在做的事情。”

今年夏天，小野将作为技术顾问参加巴黎奥运会。除了校队之外，小野还提供基于数据的运动提高课程，在学校很受欢迎。

作为一名理论数学家，小野的职业道路本来就很孤独。但当数学老师来教体育课时，两个世界之间的次元墙消失了，每个世界都变得更加有趣。

参考

[1]道格拉斯，凯瑟琳，等人。 “在数据中畅游。”数学智能r46.2 (2024): 145-155。