然而简谐振动的美妙之处不仅体现在公式的各种推导上,还存在着一些奇怪的关系。今天我们就来聊聊他们。
我们已经知道,用来描述振子位移随时间变化的关系可以写成如下正弦(或余弦)函数的形式,即
不仅如此,我们还会在书中看到另一种说法,说简谐振动的运动学方程也可以用下面的复指数形式表示,即
不知道大家看到上面这两种表达方式是否感到奇怪。我认为至少有两个方面很奇怪:
弹簧振子的简谐振动是一维问题,而三角函数则源自三角学,是骨子里带有二维“基因”的几何问题。一维的事物如何用二维的术语来表达?它们之间有几何联系吗?
弹簧振荡器距平衡位置的位移应该是实数。表达式中怎么会有虚数呢?
事实上,我们得从欧拉公式和复平面开始。

美丽的欧拉公式
我们先来说说欧拉公式。欧拉公式一般表示为:
它被称为数学史上最美丽的公式之一。为什么这么说?因为当我们代入上面的公式后,我们就会得到一个神奇的公式,那就是。
它有什么美妙之处呢?因为它用极其简洁的方式将两个最重要的无理数(,)、最重要的虚数()、两个最重要的元素(0, 1)、最重要的运算符()和最重要的关系符号组合在一起() 全部相连。这实在是太了不起了,我们不禁想知道这是否是上帝创造之书中的珍贵一页。
了解了欧拉公式后,我们现在将了解它与简谐振动的关系。
复数和复平面上的点

现在请让我们重点关注欧拉公式等号右侧的部分。可以看到欧拉公式右边是两项之和,一项是实数,一项是虚数。在数学中,我们将这种形式的数字(其中 均为实数)称为复数。其中 称为复数的实部, 称为复数的虚部, 称为虚数单位。
我们都知道任何实数都可以用实数轴上的对应点来表示,但是复数可以表示吗?复数也是可能的。然而,复数与实数不同。实数只需要一维上的点,但如果要确定复数,则必须同时确定实部和虚部(即和)。因此,复数必须由两个数轴组成的平面来表示,其中之一是数轴。一个用于确定实部,另一个数轴用于确定虚部。我们称这个特殊平面为复平面。
这样,任何复数都可以找到与复平面上的点一一对应的关系,如下图所示。
上图实际上使用了两种坐标来表示复数:一种是使用点的直角坐标形式;另一种是使用点的直角坐标形式。另一种是采用点的极坐标形式,称为复数模、复数自变量。
如果两个坐标描述的是同一件事,那么这两个坐标一定是相关的,对吗?不难看出,两个坐标之间的对应关系可以通过下面两个公式来体现,即
让这个点绕一圈
死点没有什么有趣的,重要的是让它移动。例如,让该点以恒定速度绕一圈旋转。像这样。
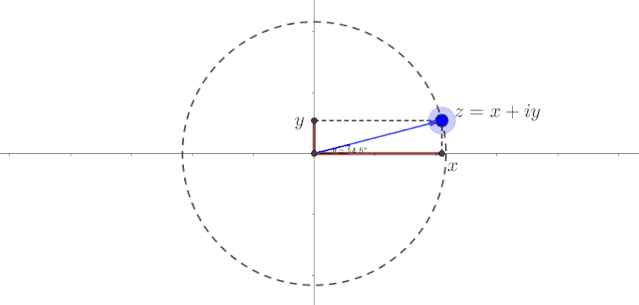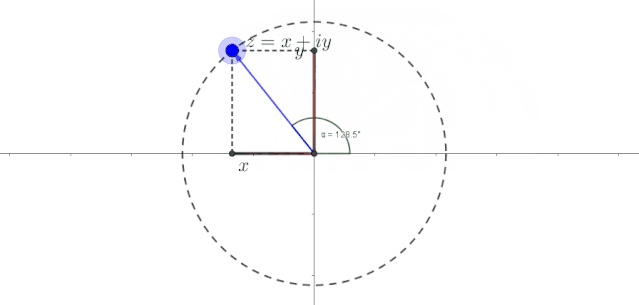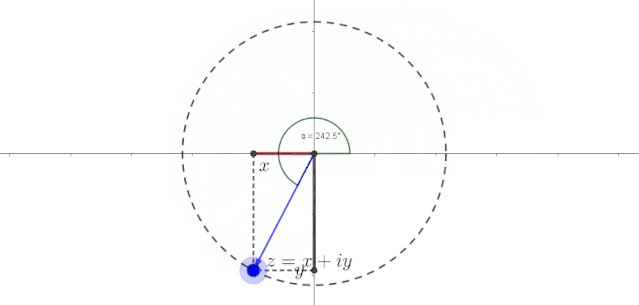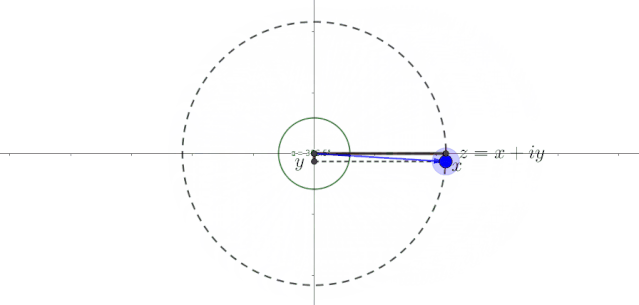
由于标出了该点的横轴坐标和纵轴坐标,我们可以直观地看到该点在匀速旋转的过程中,并且周期性地变化。它们一会儿取正值,一会儿取负值,一会儿变大,一会儿变小,两者大小的变化相反,这与正弦函数和余弦函数。这太不可思议了。简谐振动不是用正弦函数或余弦函数来表示吗?小伙子,你是不是隐约感觉匀速圆周运动和正弦、余弦函数似乎有点暧昧?
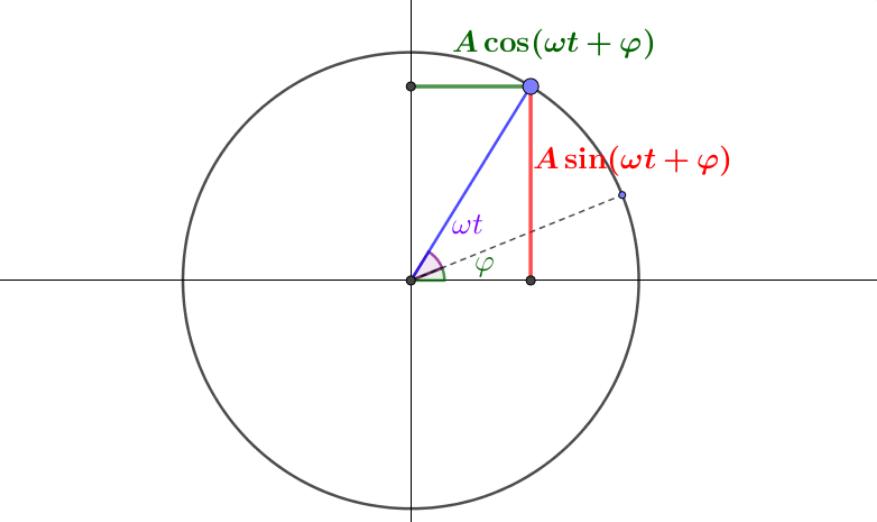
为了更详细地描述该点的匀速圆周运动,我们用极坐标来表示直角坐标。假设力矩点位于半径为 的圆上的任意位置,角为 。设该点匀速旋转的角速度为 。那么经过一段时间后,该点旋转的角度值为 。此时,任意时刻后该点的直角坐标位置应为
圆周运动与简谐振动的联系
哈哈,上面的公式不就是简谐振动的表达吗?为了直观地看到匀速圆周运动水平轴和垂直轴的变化,我创建了以下图片和动画。图中表示了粒子任意时刻的位置坐标在横轴和纵轴上的分量。可以看出,随着时间的变化,这些分量按照正弦和余弦函数变化。

在这种情况下,我们可以创建一个动画来将匀速圆周运动与简谐振动联系起来。像这样:
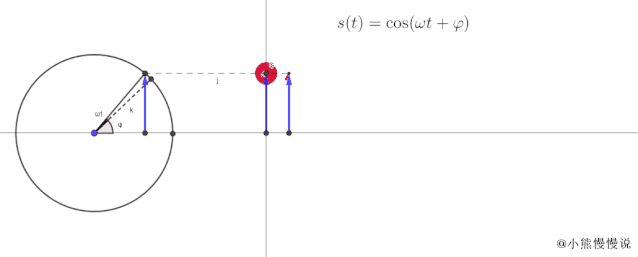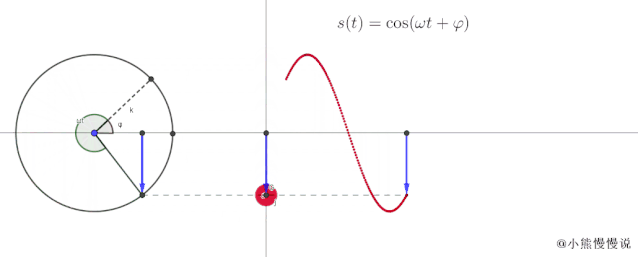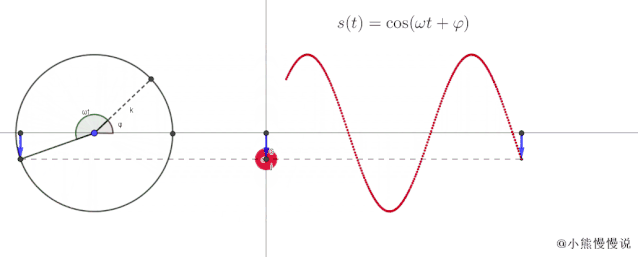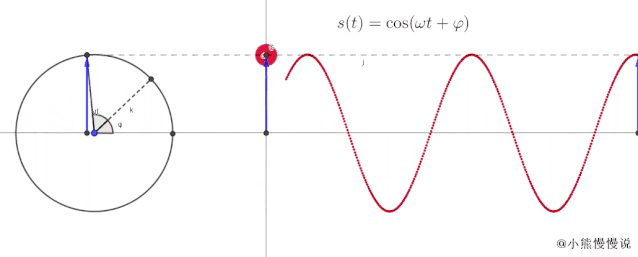
从动作中可以看出:
当一点绕半径为 的圆作匀速运动时,其水平轴和垂直轴随时间的变化与简谐振动一致;
振动函数有一个真实直观的感受,就是零时匀速圆周运动对应的初始自变量。我们称之为初始阶段,即粒子的初始位置。是以匀速圆周运动对应的初始角为基础的多次旋转的角度;
所谓振幅,实际上就是匀速圆周运动对应的轨迹半径。
以前我们学习简谐振动的时候,因为没有这样的动画来帮助我们理解,所以我们总是很困惑相位和初始相位是什么意思,以及为什么选择这个名字。那么现在有了直觉认知,对概念的理解就可以变得更深了。
简谐振动的复指数表示
我们再来说说欧拉公式的另一个作用,就是可以用复数来表示简谐振动。我们将欧拉公式替换为以下形式:
这个公式是什么意思?它表明,作为复平面上一点的复数,其实部或虚部可以用来表示简谐振动。为什么要这样做?因为用指数讨论一些复杂问题时遇到的计算比用三角函数更方便,比如阻尼振动、受迫振动等问题。
最后的话
通过上面的聊天我们可以看到,欧拉公式就像一个胶水,将简谐振动和圆周运动连接起来,让我们能够在不同类型的运动之间建立联系。而且,欧拉公式还为研究振动问题提供了一种新颖的思路。在某些问题中,可以使用三角函数来分析,而在其他问题中,使用复指数可能更方便。
数字与形状相结合的方法一直是理解物理定律和概念的法宝。有时候,很难用一句话表达的概念,只需要给出一个场景或者一个动画,就能很容易地理解概念的含义,给人一种“无声胜有声”的快感。
版权声明:本文内容由互联网用户自发贡献,该文观点仅代表作者本人。本站仅提供信息存储空间服务,不拥有所有权,不承担相关法律责任。如发现本站有涉嫌抄袭侵权/违法违规的内容, 请联系本站,一经查实,本站将立刻删除。如若转载,请注明出处:https://www.fxk666.com/html/tiyuwenda/14115.html







