初中我们把它们称为一次函数和二次函数,它们都是最简单的。通过这两个家伙,初中数学引入了函数的概念,最终将中学数学带入了变量时代。

事实上,它们都是幂函数的一种。
我们来看一下幂函数的定义:
首先必须注意的是,自变量前面的系数只能是1,如果是其他系数,就不能称为幂函数。
指数a的值是任意的,即它可以取整个实数范围内的值。因此,凡是满足上式的函数都称为幂函数。然而,我们在中学主要学习以下五种类型,即:
但实际上,在实际应用中,我们经常可以看到以下扩展函数:
既然我们研究函数,就要研究它的三大要素、五大性质,以及它们在图像上的独特表现。
为了便于研究上述函数的共同特征,我们可以先尝试画出这些函数的图像。
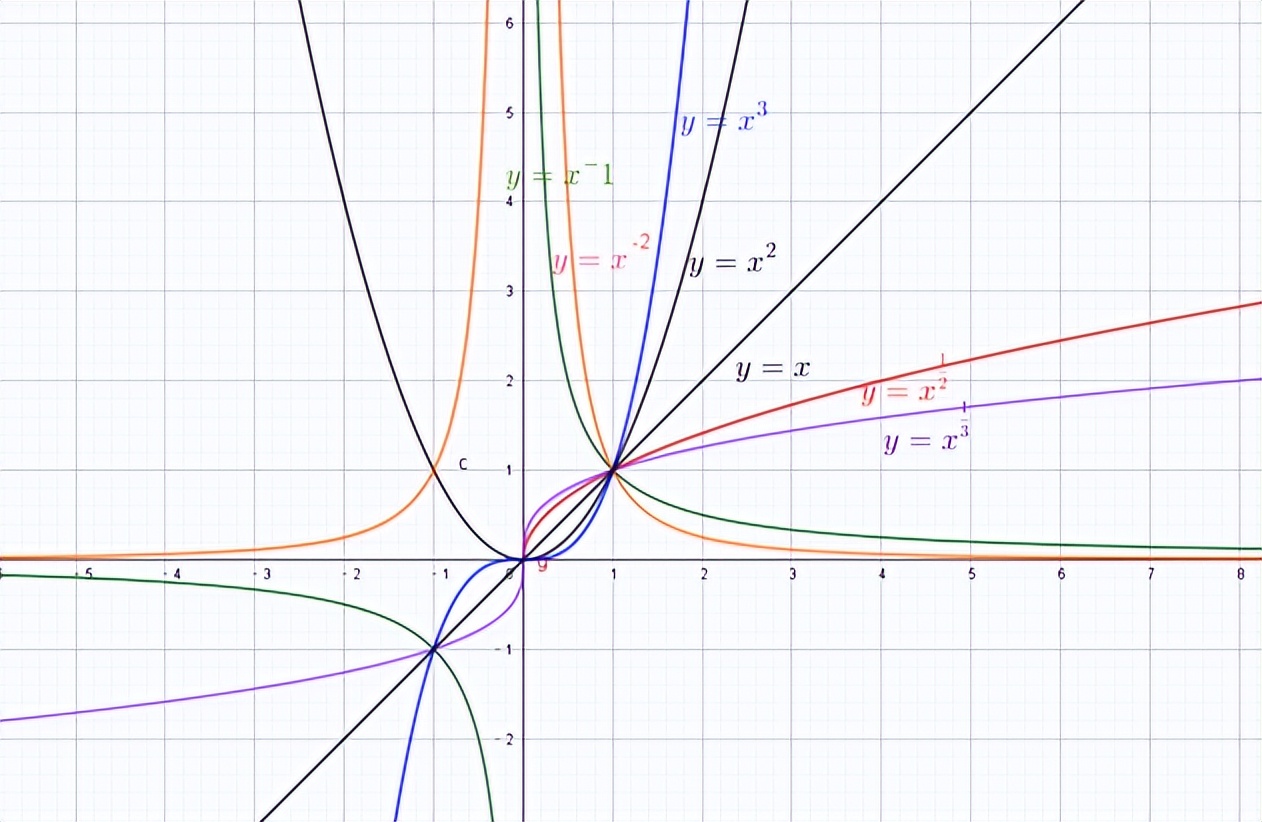
常见幂函数的图像
有了这些函数的图像,研究这些函数就变得更加直观了。
1.首先我们来说说定义域。对于幂函数,函数的定义域取决于指数的值。
当索引a
当索引a=0时,x也不能取0。
当指数a为实数的偶根时,如a=1/2,x不能小于0
但它们也有一个共同的特点,那就是它们都定义在正实数的范围内。唯一的区别是定义域是否可以扩展到0和负数。

2. 范围:所有奇函数的范围都是实数R
偶函数的范围需要进行一些划分:
索引a
当索引a=0时,为常数函数1,取值范围为1;
指数大于零的偶函数的值域是不小于0的实数。
3.用图像更容易研究这些函数的性质。
首先是单调性。在定义范围内,单调递增包括:
单调递减是这样的:
这两项是增加和减少的。增加和减少的方式不同。
比价就不用讲了,看图就知道了。
周期性不存在。至于对称性,看几个的奇偶性就可以了。
4、函数的凹凸必须要解释清楚(为了解释方便,我们以函数在第一象限的表现为例,在其他象限,可以根据函数的奇偶性去对称) : 在第一象限中,
对于指数在0到1之间的函数,第一象限的图像都是向上凸的,这说明凸函数并没有跑掉(凹凸的定义有国内外两种体系。国内的象形图这里使用定义,向上凸函数称为凸函数);
任何指数大于 1 的函数都是第一象限的凹函数。
等于1是一条直线。
5. 根据图像,所有幂函数都经过点(1, 1)。奇函数也经过点(-1,-1)。
6、所谓幂函数就是求一个变量的幂的操作,所以幂函数的一种用途就是比较大小,这在练习中经常出现:
如果指数相同,基于幂函数的单调性,可以非常简单地比较函数值。

但是如果自变量相同但指数不同怎么办?您可以通过画直线轻松比较尺寸,如图所示:
在x>1的区间内,比如通过画线x=1.5,就可以很方便的比较此时各个函数的大小。
同样,在 0
然而,比较大小时最常见的问题可能是具有不同自变量和不同指数的两个幂函数。这种情况下,我们就必须通过比较两个需要比较的函数值来找到一个合适的中间量。与中间量比较可以解决这个问题。
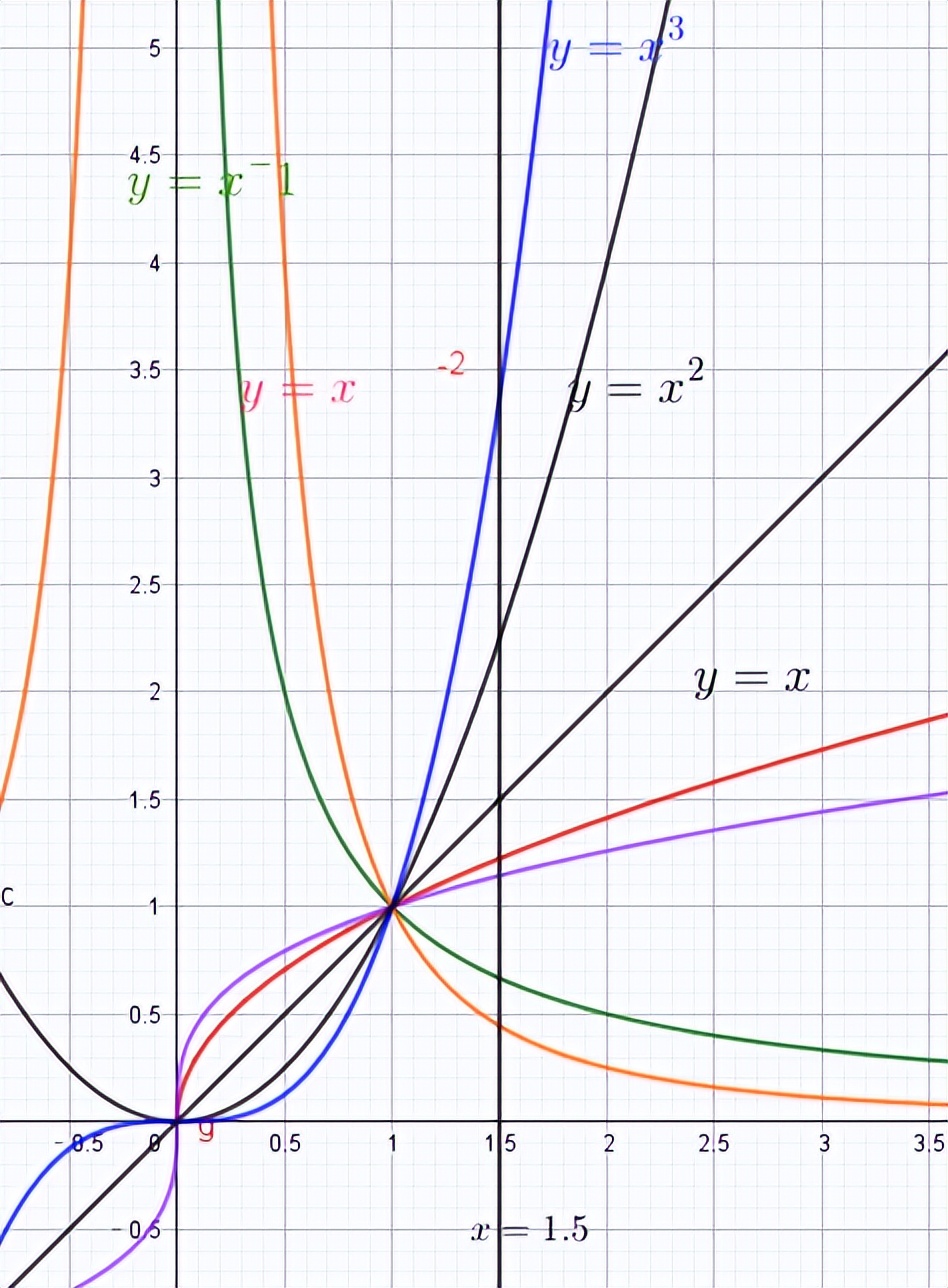
垂直线可以轻松比较函数值
7. 我们知道幂函数的指数值都是实数。根据这个定义,下面的东西也是幂函数。
但它的图像非常有趣。如果你愿意的话,你可以搜索一下它的图片来看看。反正中学不需要掌握它,所以我们只是看看它的乐趣。

当然,我们中学学到的幂函数只是表面的一根毫毛。如果你想看到幂函数的全貌,你还必须知道这个函数是怎么来的。以下是网上找到的各个历史时期权力职能发展的简要总结。历史上,著名的数学家都参与了幂函数的成长和发展。有兴趣的可以参考:
幂函数的历史可以追溯到16世纪初,当时数学家开始研究函数的幂级数展开。最早的发现是关于三角函数的幂级数展开式,由法国数学家维耶特于 1589 年发现。
17世纪,幂函数开始得到更广泛的研究。法国数学家费马在1629年提出了一种方法,可以用任意实数作为指数,得到任意幂的幂函数展开式。
这种方法称为“费马幂级数”。
18世纪,幂函数在数学和物理学中得到广泛应用。
瑞士数学家欧拉在1740年左右提出了著名的欧拉公式,将三角函数与复数联系起来,使得幂函数在复数范围内得到广泛应用。
到了19世纪,幂函数得到了进一步的研究和发展。德国数学家黎曼在1850年左右提出了一种新的数学理论,称为“复分析”。该理论使得幂函数在复数分析中得到广泛应用。同时,幂函数也广泛应用于数学分析中。幂函数可以在泰勒级数和傅立叶级数等展开式中找到。
在现代数学中,幂函数仍然是研究的热点之一。它们广泛应用于数学分析、概率论、统计学等领域。例如,在概率论中,二项式分布和泊松分布等分布函数是幂函数的离散形式。在统计学中,一些常见的分布函数,例如正态分布和卡方分布,也涉及幂函数。此外,幂函数还广泛应用于代数、几何等领域。例如,矩阵代数、群论等领域中都会涉及到幂函数的运算。
总之,幂函数作为一种基本的数学函数,其历史可以追溯到16世纪初,并广泛应用于不同领域。它的性质和理论仍在不断发展和完善,为数学和科学的发展做出了重要贡献。
版权声明:本文内容由互联网用户自发贡献,该文观点仅代表作者本人。本站仅提供信息存储空间服务,不拥有所有权,不承担相关法律责任。如发现本站有涉嫌抄袭侵权/违法违规的内容, 请联系本站,一经查实,本站将立刻删除。如若转载,请注明出处:https://www.fxk666.com/html/tiyuwenda/21433.html








