篮球在空气中自由释放能否向上运动？探讨2020年北京高考物理题_W66利来国际

*注：这里及本文其余部分所谓的“向上运动”并不是特指篮球的“垂直向上运动”，而是指篮球运动过程中速度的垂直向上速度分量。

前言

在刚刚结束的2020年北京高考中，物理卷子第14题以从高处释放旋转篮球的生活场景为素材。通过提供新的信息（空气阻力和偏转力的方向和大小），学生能够结合现有的一些知识和方法（机械能转换、力与运动的关系、力分析）来判断和推测篮球在空中的运动。问题原文如下：

14、在无风的环境下，如果有人从高处释放静止的篮球，篮球会垂直下落；如果先将篮球绕球中心的水平轴以一定的角速度（如图所示）旋转然后释放，则篮球会垂直下落。下落过程中，它偏离垂直方向，做曲线运动。原因是，旋转的篮球除了重力之外，在运动过程中还要受到空气施加的阻力。

f1 和偏转力 f2。这两个力与篮球速度v的关系大致如下：f1=k1v2，方向与篮球运动方向相反； f2=k2v，方向与篮球运动方向垂直。以下哪项陈述是正确的？

A.k1和k2是与篮球的旋转角速度无关的常数。

B、篮球能回到原来的高度，角速度与放出时相同。

C. 如果一个人站得足够高，篮球在落地之前可能会向上移动。

D、如果释放条件合适，篮球可以继续在空中水平直线运动。

本题描述的现象如图1所示。首先，对于题中的选项A，从题目信息可以看出，不旋转的篮球下落不会受到垂直于其方向的力的作用而偏转。运动，所以f2的产生与球的旋转密不可分。因此，k2与角速度有关，但仅从问题信息中无法得出力的本质原因以及与角速度的具体关系。

图1 旋转篮球在空中下落的运动

问题中的选项 B 考察学生对空气阻力起作用时能量转换过程的理解。由于机械能的减少，篮球无法回到初始高度（本文2.1节的研究表明，如果忽略空气阻力的作用，篮球会发生周期性运动，并且可以回到初始位置。空气阻力矩对其旋转的影响参见2.5节。

关于问题选项C中提到的篮球向上运动的可能性，如果我们从定性的角度来分析这个现象，在篮球下落的过程中，从受力分析可以看出，随着速度的不断增加，篮球受到f1和f2合力的垂直分力可能大于重力，因此篮球的垂直分力速度可以减小到零或者变成垂直向上，因此篮球可能会向上移动。图2描绘了在不同旋转速度下自由释放旋转篮球的运动轨迹。可以看出，随着旋转速度的增加，相同的垂直位移（y轴）对应的篮球的横向（x轴）位移变得更大。，并且会在垂直方向上做往复运动。绘制该图的理论讨论请参考2.3节。

图2 不同转速时篮球运动轨迹的变化

（理论计算图）

至于选项D中提到的“连续水平直线运动”，如果篮球的速度变为水平，空气阻力的作用会降低篮球的速度，篮球上的偏转力f2就会变小，f2不能被维护。它不断地沿着与重力相反的方向运动，所以不可能在空中继续直线水平运动。

可见，高考中该题的设置很好地考验了学生的科学思维，对于引导学生从物理的角度认识和认识生命现象起到了很好的作用。同时，这种现象并不局限于篮球，在任何其他涉及球类的运动中都很常见，比如足球中的香蕉球、电梯球等，以及乒乓球中的各种旋转技术[2, 3] 。为了进一步探讨这一现象背后的物理原理，本文将从以下几个方面进行讨论：

01 马格努斯效应及其简要证明

1672 年，牛顿在剑桥观看一场网球比赛时观察到上旋球会导致球下落得更快。相反，后旋会使球稍微向上移动并漂移一小段距离。 1852年，德国物理学家海因里希·马格努斯提出：当旋转物体的角速度矢量与其质心的速度矢量不重合时，会在垂直于两个矢量平面的方向上产生横向力。，导致物体的飞行轨迹发生偏转，这就是著名的马格努斯效应[1]。可见，马格努斯效应产生的侧向力就是篮球问题中的偏转力。

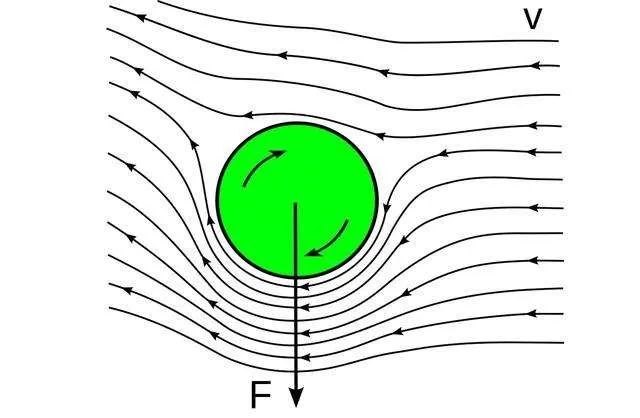
图3 马格努斯效应示意图

马格努斯效应可以用伯努利原理来解释。如图3所示，考虑一个半径为r的球相对于流体以速度v向右移动，流体相对于球以速度v向左移动。当球顺时针旋转一个角度时速度ω，其上下表面的速度方向不同。由于球体的旋转及其表面与流体之间的粘性，下端的流体会因球体同向运动的阻力而加速；反之，由于球体反向旋转的阻力，球体上端的流体速度会降低。因此，上下表面因流速差异而形成压力差，从而产生非零压力合力。该力垂直于球的旋转速度方向并垂直于相对流体的运动方向。方向是从流体通过球面流速慢的一端流向流速快的一端。简单地说，球上、下两端的流体速度vu和vd可表示为

(1)

利用伯努利方程，忽略上、下表面势能变化引起的压力差，我们有

(2)

这里 pu 和 pd 是球体上下表面的压力，ρ 是流体密度。联立式(1-2)可得

(3)

显然，该压力差与转速成正比。当转速为0时，压力差消失。进一步，从量纲分析的角度来看，物体旋转产生的压力差作用于物体表面所产生的压力合力为

(4)

其中S是球体的横截面积。上式中力的具体形式可以进一步写为F=Cρωr3 v，其中C为比例系数，可以通过球表面的面积积分得到[4-6]。需要注意的是，常数系数C还取决于流体在旋转物体表面的流动状态。因此，不同形状和表面粗糙度的物体具有不同的系数C。这里不再讨论求解过程。但该系数的具体取值并不影响式(4)中得到的力对转速ω和运动速度v的依赖性。

由式(4)得到的力即为马格努斯力，可简写为

(5)

其中比例系数

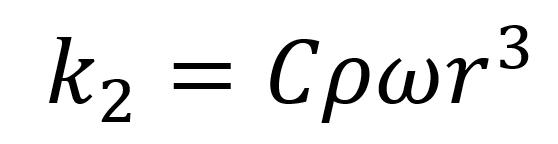
(6)

与球的速度、空气密度和体积成正比。从这个推导可以看出，马格努斯效应是伯努利原理的直接结果，与物体的旋转和平移在相对流场中密不可分。一般来说，物体旋转引起的垂直于物体平移方向的力，会导致物体的运动轨迹比没有旋转的物体更加复杂，也会有更丰富、更有趣的运动特征和轨迹。如图 4 所示，水平投掷的旋转圆柱体将向上移动，而不是显示通常的水平投掷运动轨迹。这反映了马格努斯效应对旋转物体轨迹的影响。

图4 旋转纸管在空中的飞行轨迹

可见，只要能保持圆柱体旋转，并用螺旋桨带动其前进，提供平移速度，就可以用来建造飞行器，如图5所示。

图5 利用马格努斯效应制作的飞机模型

此外，马格努斯效应还广泛应用于船舶推进装置中。图6所示的“维京格雷斯”号是一艘通过安装圆柱形转子帆以马格努斯力推进的客船。它利用发动机带动滚筒旋转，使上风侧表面气压增大，顺风侧气压减小，从而产生垂直于气流方向的侧向力。通过调节滚筒的旋转速度和方向，可以调节帆体受力的大小和方向，从而为船舶提供前进的推力[7]。综合来看，在节油和环境排放压力日益加大的情况下，旋翼辅助导航技术具有一定的应用前景。

图6 全球第一艘采用旋翼风帆技术的客船——“维京格雷斯”号

02 旋转物体的运动轨迹：

马格努斯效应的影响

在下面的研究中，我们专门考虑一个没有质心初速度且具有稳定转速的球体在空气中自由释放后的运动。运动过程中，球体质心的平移速度为v，球体绕质心的旋转速度为ω。

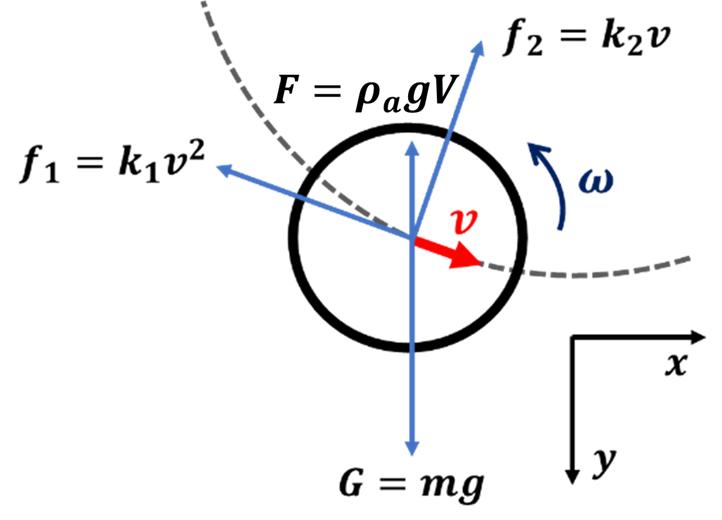
图7 空中飞行的球形物体受力示意图

如图 7 所示，为简单起见，我们考虑一个半径为 r、密度为 ρb、体积为 V=4πr3/3 的旋转球体在空气中移动。在垂直方向上，球体受到向下的重力 mg 和向上的浮力 ρagV。这两个力的大小是恒定的，与球的运动状态无关，其中ρa是空气密度。另外，球体受到与运动方向相反的空气阻力f1=k1v2，以及垂直于运动方向的马格努斯效应产生的压力差带来的马格努斯力f=2k2v。考虑球体在xy平面上的运动，可以列出以下两个运动方程

(7)

(8)

其中θ是球运动方向与x轴之间的角度，满足

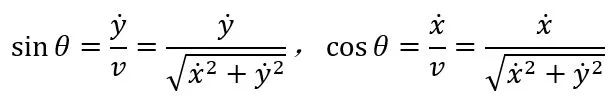
(9)

联立式(7-9)可得

(10)

(11)

对于球体，空气阻力系数和马格努斯力系数分别为

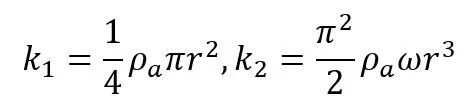
(12)

这里我们取式(6)中的C=π2/2[4]。利用上述关系式和球的质量m=ρbV=4πρbr3/3，方程（10-11）可以简化为

(13)

(14)

其中系数

(15)

这里

是空气与球体的密度比。事实上，在球运动过程中，空气会给球一个相对于质心的力矩，从而影响球的旋转速度，从而改变系数。

并影响球质心的运动。为了简单起见，在本文2.1-2.4节的讨论中，我们只关注球的质心的运动，不考虑球的转速的变化，即球的旋转速度被视为某个值。考虑空气阻力扭矩导致的转速衰减对球轨迹的影响将在2.5节中给出。

显然，根据式(15)，若

，但

，和

，此时球体（13-14）的运动方程近似为自由落体运动方程，空气阻力和马格努斯效应不明显。因此，为了清楚地看到马格努斯效应或空气阻力的影响，球体的密度需要不太高。这就是为什么证明马格努斯效应的实验通常使用密度较小的物体，例如空心球体或气球。接下来，我们首先讨论两种极端条件下的运动情况。

2.1 马格努斯力系数k2远大于空气阻力系数k1

当k2>>k1时，即球的转速ω很大时，可以忽略空气阻力的影响，只考虑马格努斯效应。那么球的运动方程可以简化为

(16)

(17)

求解这组微分方程组，可以得到满足以下条件的小球的运动轨迹：

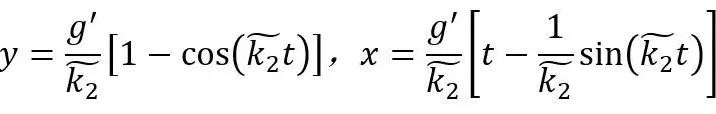
(18)

使用Matlab创建球的轨迹如下：

图8 忽略空气阻力时，旋转球体在垂直方向自由释放的运动。

图8显示，当空气阻力与马格努斯力相比可以忽略不计时，球在运动过程中几乎不耗散能量，并在xy平面上做周期性运动。由式(15)可知，此时球上下振动的频率为

，也就是说，球旋转得越快，球相对于空气的密度就越小，这种振荡运动就越快。

2.2 长时间后的稳定运动：匀速直线运动

观察图7中的受力分析，不难发现球在运动过程中可能存在稳态运动：即力平衡下的匀速直线运动。此时，球的力平衡方程为

(19)

(20)

其中，θs和vs分别表示力平衡状态下球的飞行方向与水平面的夹角和质心速度。结合上述方程组，我们可以求解

（21）

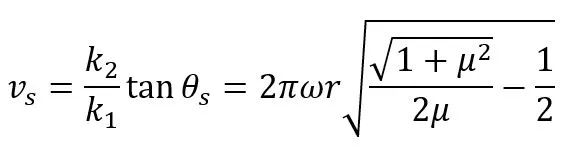
（22）

其中系数

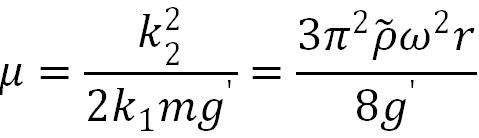
（23）

我们将力平衡状态下球体速度与水平面的夹角 θs 和运动速度 vs 分别称为闭合角和闭合速度，以及 θs 和 vs 随着转速增大的变化趋势（根据计算篮球的参数，取半径r=0.123m，质量m=0.6kg，空气密度ρa=1.29kg/m3，重力加速度g=9.8m/s2）。

图9 空气中旋转球体的闭合角度θs和闭合速度vs随球体旋转速度的变化

从图9可以看出，随着转速的增加，球体的闭合角度和闭合速度均减小，且随着速度的增加闭合角度减小得更快。这说明，当球的旋转速度越来越大时，球出手后的最终稳态运动接近于水平方向的漂移运动（与水平方向的夹角很小），因此可以在水平方向上移动更大的距离。。

特别是，当球速度ω=0时，球的运动不会发生偏转，最终在空气阻力的作用下达到匀速。此时μ→0，根据式（15），闭合角度θs=π/2，即垂直落下；另外，根据式（16），闭合速度为

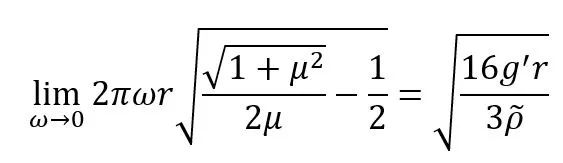
（24）

这与直接计算球体在空气阻力和重力作用下的接近速度一致[8]。

2.3 正常情况下的运动轨迹

除了上面讨论的两种特殊情况外，球的运动方程（13-14）没有通用解析解。利用Matlab对不同转速条件下的式(13-14)进行求解，得到了图10所示的几条具有不同特性的轨迹。图10中计算所使用的参数与图9中的参数一致。

2.3.1 释放无水平初速度的篮球

←a. ω=10π/s b． ω=17π/s→

←c. ω=20π/s d.ω=30π/s→

图10 没有水平初速度的自由释放旋转篮球在空中的轨迹

图10中，蓝色实线是Matlab数值求解球体动力学方程（13-14）得到的解，红色虚线是2.1节方程（18）给出的不考虑空气阻力的解析解。图10(ad)中球的旋转速度分别为ω=10π/s、17π/s、20π/s和30π/s。可以看到，在刚刚释放的小范围内，由于移动速度较小，空气阻力较小，蓝色线几乎与红色虚线重合。随着运动速度的增加，空气阻力显着增加，因为它与速度的平方成正比，导致蓝线偏离红线。

另外，比较图10c和图10d可以看出，旋转速度越大，球体在垂直方向上的下降-上升运动阶段越多。图10还表明，在运动结束时，球的轨迹趋于直线，这与2.2节给出的球的力平衡解一致。这时，球会以匀速直线运动，直到落地。

同时注意到，随着球速度的增加，球在下落过程中可能会向相反方向上升，如图10c和图10d所示，这就是第14题选项C给出的运动本文开头提到的北京高考物理卷子。场景。球上升运动条件的详细分析如图11所示。

←a.运动轨迹 B.垂直移动速度→

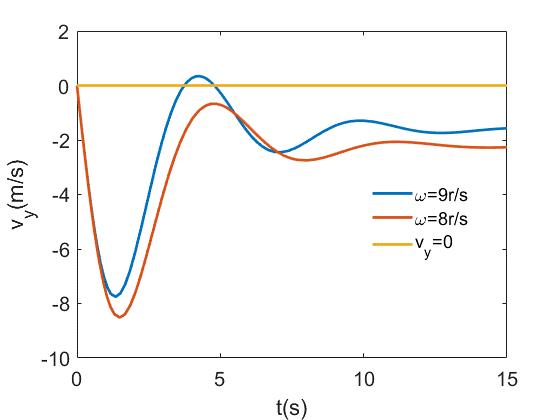
图11 空中无水平初速度的自由旋转篮球向上运动的临界条件

在图11中，我们分别绘制了旋转速度为9r/s和8r/s的篮球的运动轨迹（a）和垂直运动速度随时间的变化（b）。从运动轨迹可以看出，篮球是否会上升的临界速度点在8r/s~9r/s之间。从图 11b 可以看出，旋转速度为 9 r/s 的篮球在投掷后约 5 s 左右，在 y 轴正方向有速度，即向上运动，而8转/秒的转速不存在vy > 0的部分。同时，观察图10a可以发现，篮球向上运动的临界点对应的垂直位移在15米到20米之间。因此，为了实现文章开头标题中提到的选项C的场景，投掷的篮球高度需要距离地面至少15m，并且旋转速度需要大于8r/s 。

2.3.2 以一定的初速度释放篮球

图 12 显示了以 vx(0)=0m/s（蓝色实线）和一定水平初速度 vx(0)=20m/s（橙色实线）自由抛出的旋转球的运动轨迹。对比。在图12(ad)中，球的旋转速度分别设置为ω=10π/s、17π/s、30π/s和80π/s。

←a. ω=10π/s b． ω=17π/s→

←c. ω=30π/s d． ω=80π/s→

图12 水平抛向空中的旋转篮球的轨迹

从图12可以看出，当初始角速度相同时，与没有水平初速度的情况相比（对比图12b中的橙线和蓝线），当以一定的水平初速度释放篮球时，最初是垂直方向的马格努斯力将大于球的重力。这时，球开始“抬头”，即向上运动，到达最高点后才开始下降。并且当转速增加时，球的运动变得复杂。此时，由于马格努斯力和空气阻力的共同作用，球会在空中多次上升和下降，甚至出现螺旋状运动，如图12c和图12d所示。显示。

2.4 圆周运动和螺旋运动

值得一提的是，在旋转球的所有轨迹中，都会有圆周运动和螺旋运动。当抛出的球的密度与空气的密度相等时，即ρa=ρb，球在垂直方向上的重力和浮力平衡，即g'=0。此时小球运动方程(13-14)变为

(25)

(26)

此外，如果忽略空气阻力，球仅受到马格努斯力的作用，该力始终垂直于速度方向。不难推断，在这种情况下，小球会在马格努斯力的作用下做匀速圆周运动，如图13所示。

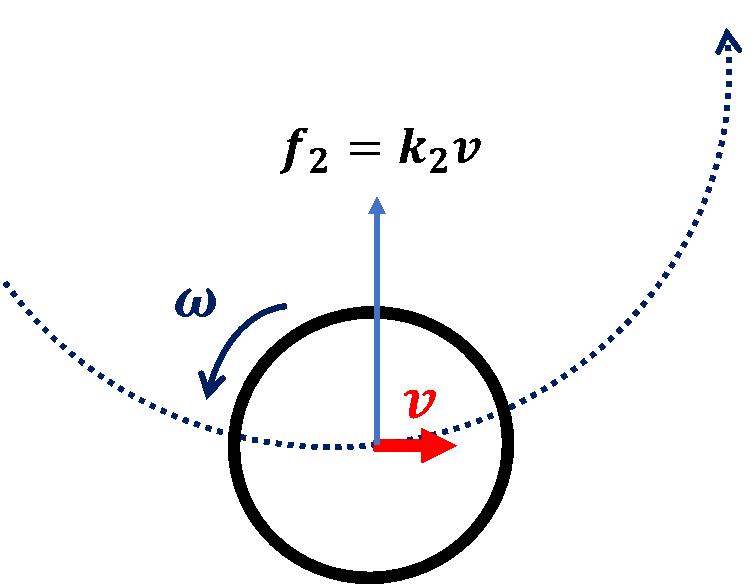
图13 旋转球体仅在马格努斯力作用下做匀速圆周运动。

利用马格努斯力提供向心力，很容易写出

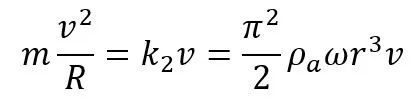
(27)

其中R是球圆周运动的半径，解为

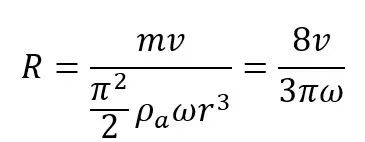
(28)

这是一个有趣的结果。这时，马格努斯力就会导致这样一个旋转的球体

(29)

旋转速度做圆周运动。该结果可以使用水平面上的旋转球体进行实验测试。这种运动状态类似于磁场中带电粒子由于洛伦兹力而作匀速圆周运动的情况。

另一方面，如果考虑空气阻力的影响，球体在做圆周运动时速度会衰减，圆的半径会减小，因此会呈现螺旋轨迹。在图14中，通过数值求解方程（25-26），我们分别给出

以及考虑空气阻力的旋转球的运动。图中计算所用球的旋转速度为ω=10π/s，球的初始水平弹丸速度为vx(0)=10m/s（蓝色实线）且vx(0)=20m /s（橙色实线）。金属丝）。

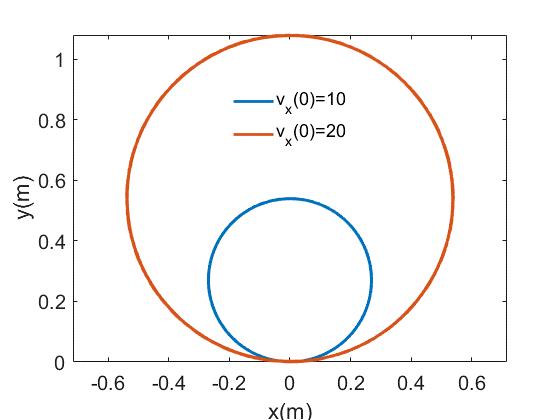
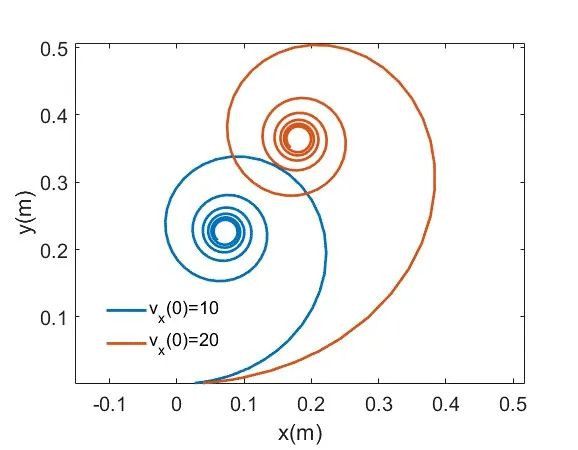
←a.无空气阻力的圆周运动

b.包含空气阻力的螺旋运动 →

图14 垂直方向（y方向）力为0时旋转球的运动轨迹

观察图14(a)可以看出，当忽略空气阻力时，小球确实做圆周运动，且圆周运动的半径与弹丸速度成正比，这与式(28)的理论结果一致）。图14（b）显示，考虑空气阻力后，球的运动轨迹是螺旋型的，并且随着投掷速度的增加，螺旋轨迹的大小增加。

2.5 空气阻力矩的影响

在前面的讨论中，我们假设球的旋转速度是恒定的，那么球上的马格努斯力的系数k2也是恒定的，因此球上的马格努斯力只会因为球的速度的变化而变化。球的质心。但在实际投球情况下，球的旋转速度会因空气阻力力矩的存在而衰减，从而通过影响马格努斯力系数k2的大小来影响球的运动，从而改变轨迹球的。一般来说，空气中旋转的物体所受到的阻力矩与物体的速度呈正相关。最常用的阻力矩模型一般认为阻力矩与速度的一次方或二次方成正比，即

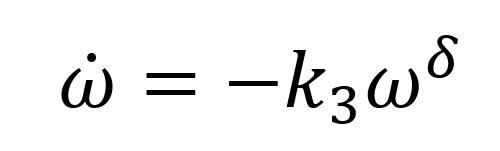
(30)

其中，δ=1,2，k3为空气阻力矩系数。将上式与式（13-14）结合起来，可以求解转速衰减情况下球体的运动。相应的运动轨迹如图15所示。球的初始旋转速度设置为ω=40π/s。

←a.空气阻力扭矩与速度成正比

b.空气阻力扭矩与速度的平方成正比→

图15 空气阻力矩对自由释放旋转球体运动轨迹的影响

从图15可以看出，考虑阻力矩后，由于马格努斯效应随着转速的衰减而减弱，球在垂直方向上反向运动的次数会减少。另外，比较图15b和图15a可以看出，当阻力矩与转速的平方成正比时，垂直方向的振荡运动的衰减更加迅速。同时，图中的轨迹也表明，考虑转速衰减后，在相同垂直位移下，小球对应的横向运动随着转速衰减的增大而减小。

综上所述

总体来说，北京2020年高考物理卷子第14题是从高空释放旋转篮球的生活场景开始的。它通过赋予新知识，考察考生结合现有知识并学会应用新知识解释物理现象、探索物理学的能力。问题能力。本文进一步分析了该主题所涉及的马格努斯效应，并特别讨论了在不同条件下释放出空气中旋转篮球的轨迹，并得出以下结论：

（1）空气中旋转球体所经历的偏转力是马格努斯力，可以根据伯努利的原理进行解释，并推导其特定形式，即f =cρωr3v，它与物体的旋转速度成正比，相对流体的速度和物体的体积。成比例。马格努斯效应可用于制造具有特定结构的飞机，也可以用作船舶上的推进装置，以节省能源消耗。

（2）当释放高度合适并且与马格努斯力相比，空气电阻可以忽略不计时，旋转球会在平面上上下进行周期性运动；

（3）当释放高度合适时，旋转球最终将在运动过程中达到均匀的线性运动状态。随着旋转速度的增加，在这种均匀的线性运动中，球体的结尾角和终端速度均降低，并且随着速度的增加，末端角度降低了。

（4）根据数值计算结果，当释放高度至少达到15m并且球的初始旋转速度大于8R/s时，旋转球将在运动过程中向上移动；

（5）当旋转球以较大的水平初始速度投掷时，球将首先向上移动；

（6）当扔球的密度不考虑空气和空气电阻的密度时，旋转球将圆移动。测量空气电阻时，球的轨迹是一种螺旋。

（7）如果考虑到空气阻力扭矩对释放球旋转的减速效应，则将减少在马格努斯力的作用下球的横向位移。

参考

[1] Resnick R，Halliday D，Krane KS。物理［m ］． John Wiley＆Sons Inc，2002年。

[2] Jiang Xinyi，Lu Jianfeng。 MATLAB模拟了异常足球运动及其实际应用[J]。大学物理学，2019年（11）。